Pembahasan Soal OSN-K Matematika SMA 2023

Pembahasan OSN-K Matematika SMA 2023

Olimpiade Sain Nasional (OSN) SMA Tahun 2023 tingkat Kabupaten/Kota telah selesai di selenggarakan serentak secara nasional pada tanggal 5 - 6 April 2023. Matematika merupakan salah satu bidang yang dilombakan dalam OSN.

Beberapa tips yang berguna untuk persiapan menghadapi OSN K matematika SMA

• Pelajari dengan seksama materi yang diujikan dalam OSN K matematika SMA, seperti aljabar, geometri, trigonometri, dan kalkulus. Pastikan Anda memahami setiap konsep secara mendalam.
• Gunakan buku-buku referensi yang berkualitas.
• Praktikkan soal-soal yang sering muncul dalam OSN K matematika SMA, terutama soal-soal yang membutuhkan pemikiran kreatif dan solusi yang tidak langsung.
• Bergabunglah dengan kelompok belajar atau bimbingan privat yang mengkhususkan diri dalam persiapan OSN. Anda dapat memanfaatkan pengetahuan dan pengalaman para tutor atau teman sebaya dalam memperkuat pemahaman dan keterampilan matematika Anda.
• Terakhir, jangan lupa berlatih dengan konsisten dan teratur, serta jangan menyerah meskipun menghadapi kesulitan. Ingatlah bahwa persiapan matang dan tekad yang kuat adalah kunci kesuksesan dalam OSN K matematika SMA.

Karena evennya sudah selesai maka tidak ada salahnya jika kita membahas soal-soal yang diujikan dalam OSN Matematika SMA Tingkat Kabupaten/Kota Tahun 2023. Berikut kami bagikan soal-soal OSN-K Matematika SMA Tahun 2023 yang telah kami rangkum dari berbagai sumber. Soal OSN-K Matematika SMA ini terdiri dari beberapa paket soal (soal berbeda tapi dengan jenis dan tingkat kesulitan yang sama). Jadi bila soal yang kami sajikan berbeda maka itu berarti soal dari paket yang berbeda. Mari kita simak-soal-soalnya!

Soal OSN-K Matematika SMA Tahun 2023

Soal No.1 (#OSN-K 2023)

Hasil penjumlahan semua solusi persamaan @$\left | x-\left | 2x+9 \right | \right |=99@$ adalah ...

Penyelesaian:

Definisi nilai mutlak

Jika @$\left | f(x) \right |=a @$, maka:
@$f(x)=a@$, untuk @$f(x)\geqslant 0@$, dan @$f(x)=-a@$ untuk @$f(x) < 0 @$

#untuk @$f(x) = a@$ maka:
@$ x-\left | 2x+9 \right | =99@$
@$ x-99=\left | 2x+9 \right |@$
Syarat: @$ x-99 \geqslant 0@$ maka:
@$ x \geqslant 99@$
@$(x-99)^2=\left | 2x+9 \right |^2@$
@$(x-99)^2=( 2x+9 )^2@$
@$(x-99)^2-( 2x+9 )^2 = 0@$
@$(x-99+2x+9)(x-99-2x-9 ) = 0@$
@$(3x-90)(-x-108) = 0@$
@$x=30@$ (TM) atau @$x=-108@$ (TM)

#untuk @$f(x) = -a@$ maka:
@$ x-\left | 2x+9 \right | = -99@$
@$ x+99=\left | 2x+9 \right |@$
Syarat: @$ x+99 \geqslant 0@$ maka:
@$ x \geqslant =99@$
@$(x+99)^2=\left | 2x+9 \right |^2@$
@$(x+99)^2=( 2x+9 )^2@$
@$(x+99)^2-( 2x+9 )^2 = 0@$
@$(x+99+2x+9)(x+99-2x-9 ) = 0@$
@$(3x+108)(-x+90) = 0@$
@$x_1=-36@$ atau @$x_2=90@$ (Keduanya memenuhi syarat)

Jadi jumlah semua solusinya adalah:
@$x_1 + x_2=-36+90 = 54@$

Jawaban: 54

Soal No. 2 (#OSN-K 2023)

Di dalam suatu laci, terdapat sembilan pasang kaos kaki yang setiap pasangnya berbeda dengan pasangan lainnya. Diambil empat kaos kaki sekaligus secara acak. Banyaknya cara pengambilan sehingga di antara yang terambil terdapat tepat sepasang kaos kaki yang cocok (berpasangan) adalah …

Penyelesaian:

Di dalam suatu laci, terdapat sembilan pasang kaos kaki yang setiap pasangnya berbeda dengan pasangan lainnya. Diambil empat kaos kaki sekaligus secara acak. Banyaknya cara pengambilan sehingga di antara yang terambil terdapat tepat sepasang kaos kaki yang cocok (berpasangan) adalah …

Penyelesaian:

Diketahui 9 Pasang kaos kaki (18 Kaos)

Kata kunci: tepat sepasang kaos kaki yang cocok (berpasangan)

Artinya: Bila diambil 4 kaos kaki maka 2 kaos harus sepasang, dan 2 lainnya tidak boleh sepasang.

Banyaknya cara mengambil 4 kaos dari 9 pasang adalah: @$_{1}^{9}\textrm{C} \times{} _{2}^{8}\textrm{C} \times 2 \cdot 2 = 9 \times 28\times 4 =1008@$

Jika sobat memmiliki jawaban yang lain silahkan dishare di kolom komentar!

Soal No. 3 (#OSN-K 2023)

Diberikan trapesium ABCD dengan AB = 14, CD = 17, AB sejajar CD, dan kedua sudut @$\angle ADC@$ dan @$\angle BCD@$ kurang dari @$90^\circ @$. Misalkan P dan Q titik yang terletak pada sisi CD sehingga AD = AP dan BC = BQ

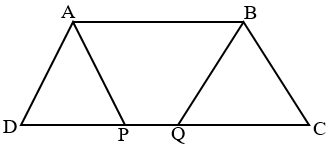
Panjang PQ = ….

Penyelesaian:

Perhatikan gambar berikut!

Berdasarkan gambar bisa kita peroleh: @$x+y=DC-AB=17-14=3@$

Sehingga @$PQ = AB - (x+y) = 14-3=11@$

Jawaban : 11

Soal No. 4 (#OSN-K 2023)

Suatu bilangan 4 digit 9ab9 merupakan suatu bilangan kuadrat. Nilai a+b adalah …

Penyelesaian:

Misal: @$9ab9 = k^2@$

Bilangan terkecil dari 9ab9 adalah 9009

Sehingga @$9009 \leq k^2 < 10000@$

@$94 < k < 100@$

@$k=97\rightarrow k^2=9409@$

sehingga @$9ab9 = k^2 = 97^2=9409@$

@$a= 4@$ dan @$b = 0@$, sehingga @$a + b = 4 + 0 = 4@$

Jawaban: 4

Soal No. 5 (#OSN-K 2023)

Diberikan fungsi kuadrat @$f(x)=a{{x}^{2}}+bx+c@$ yang memenuhi @$f(3)=9@$ dan @$f(8)=64@$. Jika @$a\ne 1@$, nilai dari @$\frac{c-b}{a-1}@$ adalah ….

Penyelesaian:

@$f(x)=a{{x}^{2}}+bx+c@$

@$f(3)=a{{3}^{2}}+b.3+c=9@$

@$9a+3b+c=9@$ ...(1)

@$f(8)=a{{8}^{2}}+b.8+c=64@$

@$64a+8b+c=64@$... (2)

Eliminasi

@$64a+8b+c=64@$
@$9a+3b+c=9@$

---

@$55a+5b=55@$
@$5b=55-55a@$
@$b=11-11a@$ ...(3)

@$9a+3(11-11a)+c=9@$

@$9a+33-33a+c=9@$ @$c=24a-24@$

@$\frac{c-b}{a-1}=\frac{24a-24-(11-11a)}{a-1}@$
@$=\frac{35a-35}{a-1}@$
@$=\frac{35(a-1)}{(a-1)}=35@$

Jawaban: 35

Soal No. 6 (#OSN-K 2023)

Dua tim A dan B bertanding sepak bola sebanyak 11 kali. Pada setiap pertandingan, tim yang berhasil mencetak 6 gol pertama menjadi pemenang dan tidak ada pertandingan yang berakhir seri. Selama 11 pertandingan tersebut, tim A memenangkan pertandingan lebih banyak dibandingkan tim B, namun banyak gol yang dicetak tim B lebih banyak dibandingkan tim A. Selisih total gol terbesar yang mungkin dicetak kedua tim tersebut adalah ….

Penyelesaian:

Selisih Gol = @$B-A@$ (karena gol B lebih banyak)

Kemenangan A lebih banyak dari B, maka kemenangan B paling banyak 5 kali dan kemengan A sedikitnya 6 Kali

Agar selisih gol besar maka:

• ketika B menang skor harus 6 - 0 (selisih 6)
• ketika B kalah skor harus 5 - 6 (selisih -1)

Sehingga:

@$B- A= 5\times 6 + 6(-1)=30-6=24@$

Jawaban: 24

Soal No. 7 (#OSN-K 2023)

Diberikan segitiga lancip ABC dengan AB = 12 dan AC = 10 dan D suatu titik pada sisi BC. Misalkan E dan F menyatakan titik-titik berat segitiga ABD dan ACD. Jika luas segitiga DEF adalah 4, maka panjang sisi BC adalah @$\sqrt{n}@$ dengan @$n@$ = ….

Penyelesaian:

Perhatikan gambar berikut!

Misal: @$[ABG]=[AGD]=a@$ dan @$[ADH]=[AHC]=b@$
Dari teorema garis berat diperoleh:
@$\frac{DI}{DA}=\frac{1}{3} dan \frac{EF}{GH}=\frac{2}{3} \Rightarrow \frac{[DEF]}{[AGH]}= \frac{2}{9}@$

Sehingga:
@$[DEF]=\frac{2(a+b)}{9}=4@$
@$a+b=18@$
@$[ABC]=2(a+b)=36@$

Dengan menggunakan trigonometri diperoleh:
@$[ABC]=\frac{1}{2}\cdot AB\cdot AC\cdot \sin{\angle BAC}@$
@$36=\frac{1}{2}\cdot 12\cdot 10\cdot \sin{\angle BAC}@$
@$\frac{3}{5}=\sin{\angle BAC}@$

Karena @$\angle BAC@$ lancip maka @$\cos {\angle BAC} = \frac{4}{5}@$, sehingga dengan menggunakan aturan Cosinus diperoleh:

@$BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot \cos {\angle BAC} @$
@$(\sqrt{n})^2=12^2+10^2-2\cdot 12\cdot 10\cdot \frac{4}{5} @$
@$n=144+100-192 @$
@$n=52 @$

Jawaban: 52

Soal No. 8 (#OSN-K 2023)

Sisa pembagian @${5}^{2022}+{11}^{2023}@$ oleh 64 adalah ….

Penyelesaian:

@$5^{2022}+11^{2023}= x \mod(64)@$
Konsep: cari @$a^p=1\mod(64)@$
@$5^1=5\mod(64)@$
@$5^2=25\mod(64)@$
@$5^3=61\mod(64)@$
@$5^4=49\mod(64)@$
@$5^5=53\mod(64)@$
@$5^6=9\mod(64)@$
@$5^7=45\mod(64)@$
cari sampai
@$5^{16}=1\mod(64)@$
Sehingga: @$2022 = 16\cdot 126+6@$
@$5^{2022}=5^{16\cdot 126+6} \mod(64)@$
@$5^{2022}=5^{16\cdot 126}\cdot5^{6} \mod(64)@$
@$5^{2022}=1\cdot5^{6} \mod(64)@$
@$5^{2022}=9\mod(64)@$
Selanjutnya:
@$11^1=11\mod(64)@$
@$11^2=57\mod(64)@$
@$11^3=51\mod(64)@$
@$11^4=49\mod(64)@$
@$11^5=27\mod(64)@$
@$11^6=41\mod(64)@$
@$11^7=3\mod(64)@$
cari sampai
@$11^{16}=1\mod(64)@$
Sehingga: @$2023 = 16\cdot 126+7@$
@$11^{2023}=11^{16\cdot 126+7} \mod(64)@$
@$11^{2023}=11^{16\cdot 126}\cdot11^{7} \mod(64)@$
@$11^{2023}=1\cdot11^{7} \mod(64)@$
@$11^{2023}=3\mod(64)@$
@$5^{2022}+11^{2023}=9\mod(64)+ 3\mod(64)@$
@$5^{2022}+11^{2023}=9+3\mod(64)@$
@$5^{2022}+11^{2023}=12\mod(64)@$
Jadi sisanya adalah 12

Jawaban: 12

Soal No. 9 (#OSN-K 2023)

Diberikan suku banyak dengan koefisien bulat @$P(x)@$. Jika @$P(r_1)=P(r_2)=240@$ dengan @$r_1@$, @$r_2@$ merupakan akar-akar persamaan @$x^2+x-21=0@$, maka sisa pembagian @$P(1)@$ oleh 19 adalah ….

Penyelesaian:

Diketahui:
@$r_1,r_2@$ akar dari @$x^2+x-21@$

Karena @$P(r_1)=P(r_2)=240@$ maka:

@$P(x)=(x-r_1)(x-r_2)Q(x)+240@$
@$P(x)=(x^2+x-21)Q(x)+240@$
@$P(1)=(1^2+1-21)Q(x)+240@$
@$P(1)=-19Q(x)+240@$

Sehingga:
@$P(1)=P(1)\mod(19)@$
@$P(1)=-19Q(x)+240 \mod(19)@$
@$P(1)=-19Q(x)+19\cdot 12+12 \mod(19)@$
@$P(1)=0+0+12 \mod(19)@$
@$P(1)=12 \mod(19)@$

Jadi Sisanya = 12

Jawaban: 12

Soal No. 10 (#OSN-K 2023)

Banyaknya bilangan 4-digit yang habis dibagi 3 dan memuat angka 6 adalah ….

Penyelesaian:

Ciri bilangan habis dibagi 3: jumlah semua digit habis dibagi 3.

Bilangan 4 digit habis di bagi 3:
1002, 1005, ... , 9999
@$U_n = a + (n-1)b@$
@$9999 = 1002 + (n-1)3@$
@$9999 = 999 + 3n@$
@$3n = 9000@$
@$n = 3000@$
Jadi ada 3000 bilangan.

Bilangan habis dibagi 3 yang tidak mengandung angka 6:

- Digit pertama dapat diisi dengan 8 cara
- Digit kedua dapat diisi dengan 9 cara
- Digit ketiga dapat diisi dengan 9 cara
- Setiap kombinasi 3 digit sebelumnya digit keempat hanya dapat diisi dengan 3 cara.

Banyak bilangan yang habis dibagi 3 dan tidak mengandung angka 6 adalah 8.9.9.3 = 1944

Banyak bilangan yang habis dibagi 3 dan mengandung angka 6 adalah 3000 - 1944 = 1056

Jawaban: 1056

Soal No. 11 (#OSN-K 2023)

Misalkan ABCD segiempat talibusur dengan lingkaran luar @$\omega @$ dan BC = CD. Diagonal AC dan BD berpotongan di titik E dan diketahui bahwa BE = 8 dan DE = 5. Jika garis singgung @$\omega @$ di titik A memotong perpanjangan diagonal BD di titik P, maka @$\frac{PD}{PB}@$ dapat dituliskan dalam bentuk @$\frac{m}{n}@$ dengan @$m@$, @$n@$ bilangan asli yang relatif prima. Nilai dari @$m+n@$ adalah ….

Penyelesaian:

Mari kita perhatikan gambar berikut:

Karena @$BC = CD@$, maka @$\angle BAC = \angle CAD@$, akibatnya @$AC@$ merupakan garis bagi @$\angle BAD@$. Sehingga pada segitiga @$ABD@$ garis @$AE@$ merupakan garis bagi, maka berlaku: @$\frac{AB}{AD}=\frac{BE}{DE}=\frac{8}{5}@$.

Titik A merupakan titik singgung PA pada @$\omega@$, sehingga berlaku sudut lancip antara garis singgung dengan tali busur melalui titik singgung besarnya sama dengan sudut keliling menghadap tali busur tersebut, sehingga @$\angle{PAD}=\angle{PBA}@$. Perhatikan juga @$\angle{APD}=\angle{APB}@$. Jadi Segitiga @$APD@$ sebangun dengan segitiga @$APB@$, maka diperoleh perbandingan @$\frac{PD}{PA}=\frac{AD}{AB}=\frac{5}{8}@$

Dari power of point di dapat @$PA^2 = PD\cdot PB@$. Karena @$\frac{PD}{PA}=\frac{5}{8} \rightarrow PA=\frac{8}{5}PD@$, maka:

@$PA^2 = PD\cdot PB@$
@$(\frac{8}{5}PD)^2 = PD\cdot PB@$
@$\frac{64}{25}PD^2 = PD\cdot PB@$
@$\frac{64}{25}PD = PB@$
@$\frac{PD}{PB} = \frac{25}{64}@$

Sehingga @$\frac{PD}{PB} = \frac{25}{64}= \frac{m}{n}@$, @$m=25@$ dan @$n =64@$

Jadi @$m+n=25+64=89@$

Jawaban: 89

Soal No. 12 (#OSN-K 2023)

Jika bilangan asli @$x@$ dan @$y@$ memenuhi persamaan @$x(x-y)=6y-5@$ maka @$x+y@$ = …

Penyelesaian:

@$x(x-y)=6y-5@$
@$x^2-xy=6y-5@$
@$x^2+5=xy+6y@$
@$x^2+5=y(x+6)@$
@$y=\frac{x^2+5}{x+6}@$
@$y=\frac{(x+6)(x-6)+41}{x+6}@$
@$y=(x-6)+\frac{41}{x+6}@$

Karena @$x, y@$ bilangan asli maka:
@$(x+6)@$ harus merupakan faktor dari 41 yaitu @$(-1, 1, -41, 41)@$

Sehingga:
@$x+6=-1@$
@$x=-7@$ (TM Karena bukan bilangan Asli)
@$x+6=1@$
@$x=-5@$ (TM)
@$x+6=-41@$
@$x=-47@$ (TM)
@$x+6=41@$
@$x=35@$ (Memenuhi)

Substitusikan ke:
@$y=(35-6)+\frac{41}{35+6}@$
@$y=30@$

Jadi @$x+y=35+30=65@$

Jawaban: 65

Soal No. 13 (#OSN-K 2023)

Misalkan @$a_1@$, @$a_2@$, @$a_3@$, … suatu barisan bilangan yang memenuhi persamaan @$a_{n+2}-a_{n+1}+a_n=\frac{n+5}{6}@$ untuk setiap bilangan asli @$n@$. Jika @$a_1=5@$ dan @$a_2=6@$ maka @$a_{2023}@$ = …

Penyelesaian:

Sedang proses pengetikan...

Soal No. 14 (#OSN-K 2023)

Diberikan himpunan @$S=\{a,b,c,d,e,f\}@$. Akan dipilih dua subhimpunan dari S yang gabungannya adalah S. Subhimpunan yang dipilih tidak harus berbeda, misalnya keduanya boleh sama dengan S. Urutan dari subhimpunan yang dipilih tidak diperhatikan, sebagai contoh pasangan subhimpunan @$(\{a,b,c\},\{c,d,e,f\})@$ sama dengan pasangan @$(\{c,d,e,f\},\{a,b,c\})@$. Banyaknya cara melakukan pemilihan adalah ….

Penyelesaian:

Sedang proses pengetikan...

Soal No. 15 (#OSN-K 2023)

Diberikan lingkaran @$\Omega @$ dan @$AB@$ suatu tali busur dari @$\Omega @$. Lingkaran @${{\omega }_{1}}@$ menyinggung @$\Omega @$ secara internal dan menyinggung AB pada titik tengahnya. Lingkaran @${{\omega }_{2}}@$ menyinggung @$\Omega @$ secara internal, menyinggung @${{\omega }_{1}}@$ secara eksternal, dan menyinggung AB.

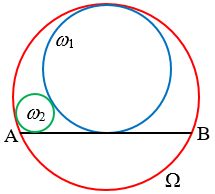
Jika jari-jari @${{\omega }_{1}}@$ adalah 45 dan jari-jari @${{\omega }_{2}}@$ adalah 9, maka panjang AB adalah …

Penyelesaian:

Sedang proses pengetikan...

Soal No. 16 (#OSN-K 2023)

Misalkan @$n={{2}^{a}}{{3}^{b}}@$ dengan @$a@$ dan @$b@$ bilangan asli. JIka hasil kali semua faktor positif dari @$n@$ adalah @$48^{27}@$, maka nilai @$ab@$ = ….

Penyelesaian:

Sedang proses pengetikan...

Soal No. 17 (#OSN-K 2023)

Nilai minimum dari @$\frac{(x+y)^2}{\sqrt{x^2-9}+\sqrt{y^2-25}}@$ adalah ….

Penyelesaian:

Sedang proses pengetikan...

Soal No. 18 (#OSN-K 2023)

Diberikan 100 titik seperti pada gambar di bawah ini.

Banyaknya persegi yang semua titik sudutnya adalah empat titik di antara titik-titik pada gambar adalah ….

Penyelesaian:

Sedang proses pengetikan...

Soal No. 19 (#OSN-K 2023)

Diberikan segitiga ABC. Misalkan D, E, F masing-masing adalah titik pada sisi BC, CA, AB sehingga AD, BE, CF berpotongan di satu titik. Diketahui bahwa @$\angle EDF=52^\circ @$. Jika @$\angle ADB-90^\circ @$ dan AF = FB maka besar sudut @$\angle ABC@$ = ….

Penyelesaian:

Sedang proses pengetikan...

Soal No. 20 (#OSN-K 2023)

Misalkan @$p@$ dan @$n@$ dua bilangan asli dengan @$p@$ bilangan prima sedemikian sehingga @$p@$ membagi @$n^2+4@$ dan @$n@$ membagi @$p^2+4@$. Jika @$p < 200@$ maka nilai terbesar yang mungkin dari @$n@$ adalah ….

Penyelesaian:

Sedang proses pengetikan...

Itulah soal OSN-K Matematika SMA Tahun 2023, untuk saat ini kami belum selesai mengerjakan pembahasannya semoga kami bisa update dalam waktu dekat. Semoga bermanfaat